Yesterday the Google Quantum AI Team with collaborators have shared a pre-print named ‘Quantum error correction below the surface code threshold’ (arXiv:2408.13687). This paper is a huge deal. I will explain why in this post1.
The whole objective of the quantum computing community is to build machines that can solve problems that are so computationally intensive for conventional computers, to be basically impossible to solve. The reason why we still don’t have any such “useful” quantum computers is two-fold: (1) classical computers have become incredibly powerful, and they set a very high bar on what problems remain untractable; (2) quantum computers don’t work as well as they should. They are plagued by errors.
Errors in quantum computing arise from both physical imperfections in the hardware and the inherent fragility of quantum information itself. Quantum computers, like all computers, process information, but they do so with quantum information, which exists in the delicate physical states of quantum systems (such as atoms, ions, or photons). These systems are so fragile and elusive that they naturally tend to lose their quantum information over time. When this loss occurs, we experience what is known as an error in the quantum computer.
Let me share an analogy: Every physical system in nature loses information over time. Another way physicists like to express this concept is by saying that ‘Entropy always increases’. One can think of information loss as a degradation process, or as the loss of ‘coherence’ — and here by coherence I mean a well-defined, ordered state2. The most familiar information loss we all experience is when we forget to put fresh food back into the fridge. In hot and humid Singapore, leaving a bottle of fresh milk on the kitchen counter overnight is a simple (and wasteful) way to experiment with information loss. Energy from the environment rapidly spreads into the milk-system, spoling its delicate order and turning it sour. A good (well-ordered) milk, became a spoiled yogurty mess.
Well, the same happens with qubits. Leave qubits out there for too long, and they will go bad. They lose information, and any attempt at performing complex computations goes nowhere.
The difference between milk and qubits, is that it takes a few hours for milk to go sour, while it takes on average a few tens of µs (~0.00001 seconds) for a qubit to lose coherence3. That’s really fast, and it means that we have very little time to use qubits before they “go bad”.
We estimate that a useful quantum computer needs to be able to run error-free for many hours, or even days, on hundreds of qubits. I am sure you can see the problem here: One day is equal to 86,400 seconds. If our qubits can remain error free for only 0.00001 seconds, we better find a way to extend their error-free lifetime or we are in troubles!
Enter quantum error correction. Quantum error correction is a procedure where by grouping together a large number of error-prone, physical qubits, we can use their collective behaviour to derive a single error-corrected qubit. We call it a “logical” qubit (because it is an abstraction and not a physical system).
Let me use another analogy, this time using football. Imagine a football team where each player represents a physical qubit in a quantum computer. Just like in football, no single player (or qubit) is perfect; they might make mistakes, get tired, or miss a play. In a game, if one player makes a mistake, it can cost the team a goal. Similarly, if a single qubit experiences an error, it could compromise the quantum computation.
To prevent this, instead of relying on just one player, you bring together a group of players (multiple physical qubits) to work together as a unit. This group, or “team,” plays in such a way that even if one or two players make a mistake, the rest of the team can cover for them, ensuring that the team’s overall performance remains strong. This group of players working together is like your logical qubit.
In quantum computing, a logical qubit is made up of multiple physical qubits that work together to protect the information they carry, much like a well-coordinated football team covers for its players. Importantly, the more players you have, and the better they work together, the less likely the team (or logical qubit) is to fail. There is strength in numbers when it comes to quantum error correction, especially if the indidual qubits are very error-prone to begin with.
Now, a fault-tolerant qubit is like a football team that is so well-trained and coordinated that even if a few players make mistakes or are temporarily out of position, the team as a whole can still play effectively without letting the opposing team score. This fault-tolerance is achieved by having a good strategy (an error correction code) and ensuring that the team (logical qubit) is large and coordinated enough to handle the inevitable errors that occur during the game.
So, just as a well-organized football team can keep playing effectively despite individual errors, a fault-tolerant logical qubit can continue to perform reliable quantum computations, even when some of its physical qubits encounter errors.
Just to conclude the analogies, keep in mind that we also perform error correction for milk. This is done using the big, noisy device you keep in your kitchen. The fridge! A refrigerator pumps heat out of the system, protecting the milk from unwanted interactions with the environment and extending its lifetime by days4. Obviously, even a fridge is not perfect, but it works for our purposes.
Let me recap now the concepts:
- Physical qubit: A qubit that suffers from errors and loses information.
- Quantum Error Correction code: A strategy to group physical qubits together to make them noise-resistant.
- Logical qubit: A ‘team’ of multiple physical qubits, working together as instructed by a quantum error correction code to protect against errors.
- Fault-tolerant logical qubit: A logical qubit that can remain error-free for a very long time.
The goal of fault-tolerant quantum error correction is to derive logical qubits with error rates that are significantly better than their constituent physical qubits5. The Google paper showed that this is experimentally possible! Let’s get into some of the details. From now the writing will become more technical, but I will do my best to explain the meaning of the (sometimes heavy) jargon.
The most impressive result of this paper is the demonstration of a below threshold surface code memory on two quantum processors (including one with more than 100 qubits!).
Let’s explain what this means!
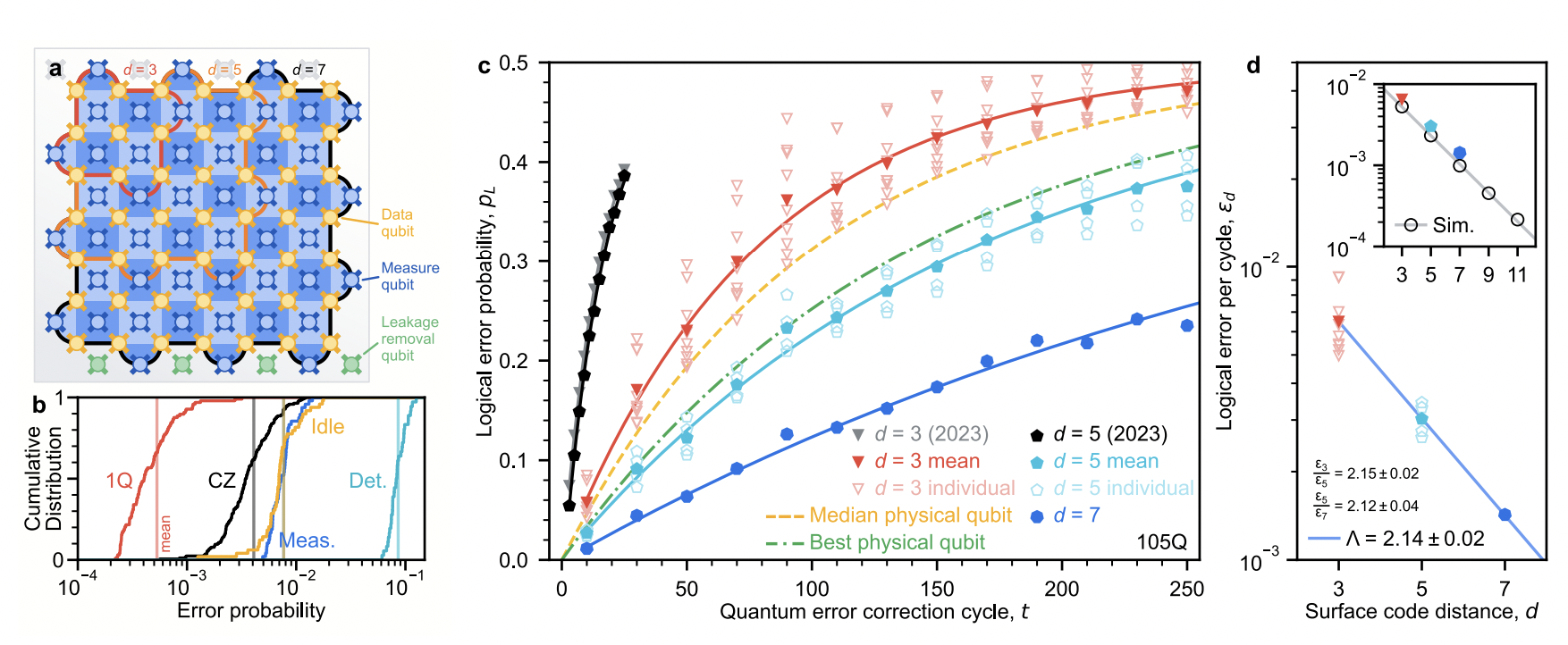
A quantum memory experiment tests the ability of a logical qubit to store and preserve quantum information over time by protecting it using a quantum error correction scheme. Here, Google used the surface code, a type of quantum error correction code designed to protect quantum information from errors by spreading it across multiple physical qubits arranged in a two-dimensional grid or lattice. The surface code is well-suited for qubits that are laid out in a planar architecture, like those in Google’s superconductin quantum computers. Below threshold means that they managed to reduce the errors happening in the physical qubits low enough (thanks to improved engineering techniques) so that the surface code can successfully reduce the overall error rate of the logical qubit.
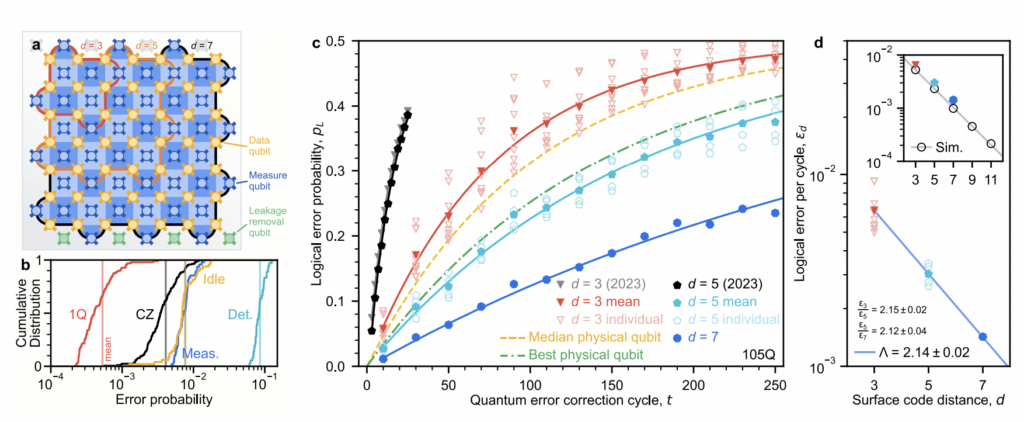
Specifically, they demonstrated a logical memory beyond break-even. It means that the logical qubit retains its quantum information longer than the best individual physical qubit in the system. The memory works! Although not forever. For a distance-7 logical qubit (defined by 7×7 = 49 physical qubits) the lifetime of the logical qubit is 291 μs, compared to an average lifetime of the best physical qubit equal to 119 μs. This is an improvement by a factor of 2.4, an increadible feat! In a way, it’s like saying that a team of 49 players gets to defend their goal much longer than any individual player would be able to (which makes sense). They also showed that the more physical qubits you include to create a logical qubit, the better it gets. The more players in your team, the stronger the team becomes.
Hopefully, the team analogy will make it simpler to understand that you can have a team but if it is not well-trained, you end up with more mistakes overall. To move towards fault-tolerant quantum error correction, we really need:
- A well-trained team. (enough team members, plus a good team management strategy — your qubits and quantum error correction code),
- Each team individual to be sufficiently fit (and this idea corresponds to the “below_threshold” part).
With these two things, you end up with a entity whose sum of parts become greater than each individual component. Putting together this latest result with Google’s results from last year7, they have showed that, effectively, we are now capable of
- Building a bigger team (more qubits!),
- Our team players are each individually well-trained enough, such that:
- Bigger team means more effective team overall. There is a progression of increasing effectiveness.
We can have scalable sport teams! Or better said, we are progressing towards scalable quantum computers8.
The demonstration of a a below-threshold surface code memory is a fantastic result for the industry. It shows that in principle, it is possible to scale the performances of a quantum processors, and reduce errors by using quantum error correction. At Entropica Labs we are busy building the software infastructure to manage the quantum error correction layer of the stack, so that we can automate all the complexities of these processes.
I am incredibly excited about the next years in quantum computing. We are likley to witness monumental shifts in what is possible to do with these devices and I can’t wait for results coming from increasingly larger and more complex processors. It’s a great time to be working in this field.
- To the experts: Here I will avoid being overly pedantic with definitions. My goal is to help anyone interested in the field to understand why Google’s is a major result for quantum computing, not to give a technical review of their work. ↩︎
- I fear what statistical physicists might say when reading this paragraph. Please forgive me. ↩︎
- Different types of qubit have different coherence-times, but none of them can last as long as milk if left on your kitchen counter. ↩︎
- Nerdy time: You can leave milk outside for about two hours, or 7,200 seconds before it goes bad. A cold fridge can extend the lifetime of fresh milk to about 7 days, or 604,800 seconds, two orders of magnitude more. Not great, not terrible. ↩︎
- Ideally, if a physical qubit has one error every 100,000 operations, we want the logical qubit to have one error every 10,000,000,000 operations. ↩︎
- Surface code performance. a, Schematic of a distance-7 surface code on a 105-qubit processor. Each measure qubit (blue) is associated with a stabilizer (blue colored tile). Red outline: one of nine distance-3 codes measured for comparison (3 × 3 array). Orange outline: one of four distance-5 codes measured for comparison (4 corners). Black outline: distance-7 code. We remove leakage from each data qubit (gold) via a neighboring qubit below it, using additional leakage removal qubits at the boundary (green). b, Cumulative distributions of error probabilities measured on the 105-qubit processor. Red: Pauli errors for single-qubit gates. Black: Pauli errors for CZ gates. Blue: Average identification error for measurement. Gold: Pauli errors for data qubit idle during measurement and reset. Teal: weight-4 detection probabilities (distance-7, averaged over 250 cycles). c, Logical error probability, pL, for a range of memory experiment durations. Each datapoint represents 105 repetitions decoded with the neural network and is averaged over logical basis (XL and ZL). Black and grey: data from Ref. [17] for comparison. Curves: exponential fits after averaging pL over code and basis. To compute εd values, we fit each individual code and basis separately [24]. d, Logical error per cycle, εd, reducing with surface code distance, d. Uncertainty on each point is less than 5 × 10−5. Symbols match panel c. Means for d = 3 and d = 5 are computed from the separate εd fits for each code and basis. Line: fit to Eq. 1, determining Λ. Inset: simulations up to d = 11 alongside experimental points, both decoded with ensembled matching synthesis for comparison. Line: fit to simulation, Λsim = 2.25 ± 0.02. ↩︎
- https://www.nature.com/articles/s41586-022-05434-1 ↩︎
- Thanks to my colleague Jing Hao Chai, who gives great feedback and helped me improve the prose of the text ↩︎